Hur hittar man den mellersta trapezformade linjen?

Ett segment av en rak linje som förbinder mitten av lateralenTrapesens sidor kallas trapesens mittlinje. Hur man hittar mellankarespeslinjen och hur den hänför sig till andra delar av denna figur kommer vi att diskutera nedan.
Mittlinjen stämningen
Rita en trapezoid där AD är en störrebas, BC - mindre bas, EF - mittlinje. Vi fortsätter grunden AD för punkt D. Rita linjen BF och fortsätt tills den skärs med fortsättningen av basen AD vid punkten O. Tänk på trianglarna ΔBCF och ΔDFO. Vinklar ∟BCF = ∟DFO som vertikal. CF = DF, ∟ BCF = ∟ FDO, eftersom ВС // АО. Följaktligen är trianglarna ΔBCF = ΔDFO. Följaktligen sidorna BF = FO.

Betrakta nu ΔABO och ΔEBF. ∟ABO är vanligt för båda trianglarna. BE / AB = ½ vid skick, BF / BO = ½, sedan ΔBCF = ΔDFO. Följaktligen är trianglarna ABO och EFB liknande. Därför förhållandet mellan sidorna EF / AO = ½, liksom förhållandet mellan de andra parterna.
Vi hittar EF = ½ AO. Det framgår av ritningen att AO = AD + DO. DO = BC som sidorna av lika trianglar, följaktligen AO = AD + BC. Därför är EF = ½ AO = ½ (AD + BC). dvs Längden av trapezans mittlinje är lika med halva summan av baserna.
Är trapezans mittlinje alltid lika med halva summan av baserna?
Antag att det finns ett speciellt fall,när EF ≠ 1 (AD + BC). Då BC ≠ DO, därför, ΔBCF ≠ ΔDCF. Men detta är omöjligt, eftersom de har två lika vinklar och sidor mellan dem. Följaktligen är stämningen sant under alla förhållanden.
Mittproblemet
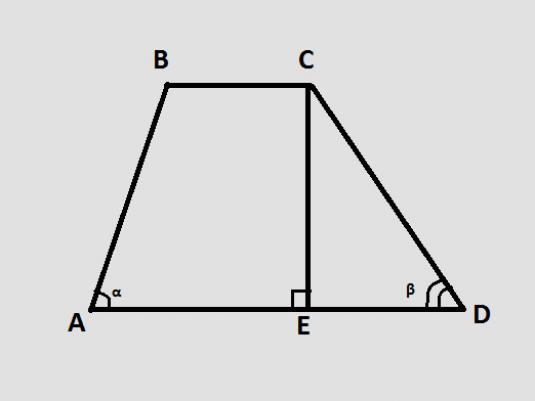
Vi antar i vårt trapezoid ABCD // AD Sun, ∟A = 90 °, ∟S = 135 °, AB = 2 cm, som är vinkelrät mot den diagonala AC-sidan. Hitta den mellanliggande trapeziska linjen EF.
Om ∟A = 90 °, då ∟B = 90 °, är ΔABC rektangulär.
∟ BCA = ∟ BCD - ∟ ACD. ∟ACD = 90 ° med villkor, därför, ∟BCA = ∟BCD - ∟ACD = 135 ° - 90 ° = 45 °.

Om i en rektangulär triangel ΔABC är en vinkel 45 °, så är benen i den lika: AB = BC = 2 cm.
Hypotenus AC = √ (АВ² + ВС²) = √8 cm.
Tänk på ΔACD. ∟ ACD = 90 ° av tillståndet. ∟CAD = ∟BCA = 45 ° som vinklarna som bildas av trapesens sekantala parallella baser. Följaktligen är benen AC = CD = √8.
Hypotenus AD = √ (AC² + CD²) = √ (8 + 8) = √16 = 4 cm.
Den genomsnittliga trapeziumlinjen är EF = ½ (AD + BC) = ½ (2 + 4) = 3 cm.