Vad är en trapeze?

Varje person som studerade i skolan, i klassengeometri, studerade vad en trapezoid. Detta ord användes även i antika Grekland och på detta språk menade "ett bord, ett bord eller en måltid". Ordet "trapezium" är en fyrkantig figur där de två sidorna är parallella, de andra sidorna är inte parallella samtidigt.

Trapezoida egenskaper

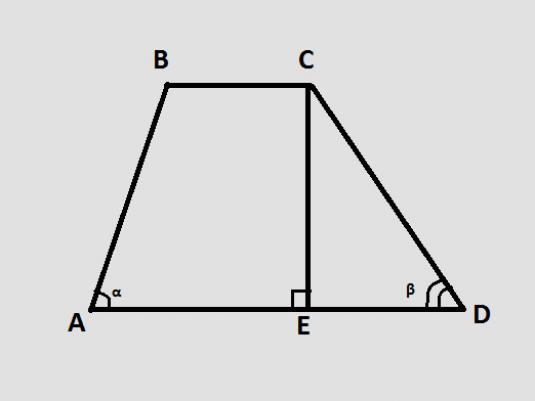
Trapesformens parallella sidor anses vara basenfigurer, och de andra sidorna är laterala. Trapezium har en mittlinje som förbinder sidorna i mitten. Också i denna figur kan du rita en vinkelrätt från en punkt på botten till den andra på den andra basen, då denna vinkelräta kallas höjden.

Det finns sådana trapezoider:

isosceles - när sidorna är desamma;
rektangulär - när sidorna av hörnen är 90 grader.

Linjen av en sådan figur, belägen i mitten,är parallellt med basen, är numeriskt lika med halva summan av de två baserna. En annan egenskap gäller vinklarna hos trapezan, nämligen summan av dessa vinklar är 180 grader.

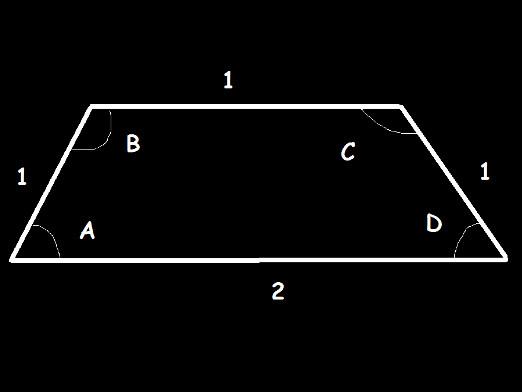
I ett jämnt trapez är de grundläggande vinklarna parvisa,till exempel vinkeln A = D och vinkeln B = C. Också i isosceles-trapeziet kommer diagonalerna som förbinder de motsatta punkterna att vara lika, vi får AC = BD.

Om summan av de två huvudsidorna i figuren är heltär identisk med summan av sidosidorna, då kan en cirkel skrivas in i en sådan figur. Dessutom är trianglarna som ligger på sidorna av trapezoiden lika.

Segmentet som ligger längs mittlinjen ochförbinder mitten av diagonalerna, är lika med hälften av skillnaden på sidorna på basen. På en linje ligger den punkt vid vilken sidosidorna skär varandra och den punkt vid vilken trapesens diagonaler sammanfogas.

område

För att ta reda på trapesformens område måste du följa denna formel:

S = (a + b) / 2 * h

I det: "a" och "in" - grunderna "h" - höjden på figuren.

Om längden på trapesformiga baser inte är kända, ochendast höjd och mittlinje, i så fall gäller följande formel: S = m * h. Där värdet av "m" är längden på mittlinjen. Dessa två formler är ekvivalenta och vi kan säga att medellinjen är m = (a + b) / 2.

Att känna området för en isosceles trapezoid,du behöver veta värdet av vinkeln. Här är formeln: S = (a - c * cos y) c * sin y = (b - c * cos y) c * sin y. Där a är lång och b är kort är c sidan och y är vinkeln mellan den långa basen och sidan.

Se även våra andra artiklar på denna sida: