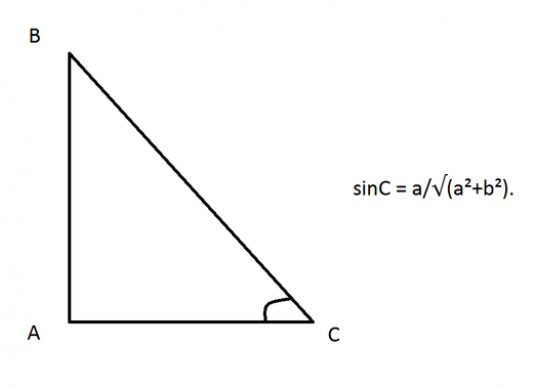Hur hittar man sinus av en spetsig trapezavinkel?

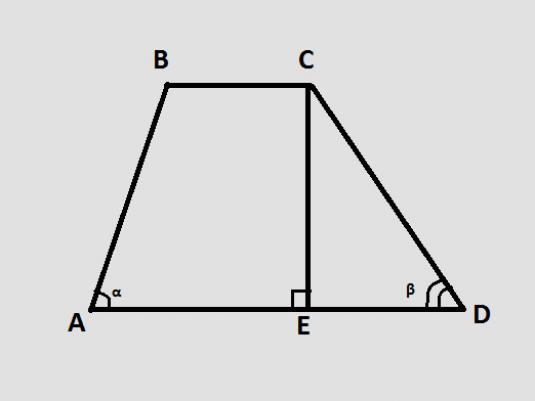
Trapezium är en fyrsidig med två sidor parallell med varandra. Tänk på hur man hittar sinus av en spetsig trapezansvinkel, med hjälp av trapesformiga ABCD som ett exempel, där sidorna AD och BC är parallella.
Vi letar efter sinus av vinkeln hos en isosceles trapezoid
Tänk på en likadana trapezoid. I ett jämnt trapez är sidorna lika. I vårt fall är AB = CD = 25 och storleken på baserna AD = 65 och BC = 51. Låt oss försöka hitta sinus av den akuta vinkeln.
Som du vet är sinus lika med förhållandet mellan det motsatta benet och hypotenusen, så vi behöver en rätt triangel. Vi klarar det genom att släppa den vinkelräta bromsen från hörnet ABC till basen.
En viktig egenskap hos trapezier är derashöjd - avståndet mellan parallella sidor, som vanligtvis kallas basen. För att bestämma detta avstånd måste du sänka vinkelrätt mot den andra basen från hörnet av den mindre (vanligtvis övre) basen. I vårt fall kommer dessa att vara perpendiculars av VN och CE, som vi behöver för att bestämma sinus.
Bestämning av trapezans höjd
Vi får två rektangulära trianglar, med benen BH = CE och hypotenus AB = CD. Följaktligen är de andra benen av dessa trianglar också lika med AH = ED.
Eftersom HB6 är fyrkantiga, är alla vinklar raka (HB och CE är vinkelräta mot baserna), då har vi fått en rektangel med sidor BC = CE.
AD = AH + HE + ED genom konstruktion. Eftersom AH = ED och HE = BC kan denna ekvation skrivas som:
- AD = 2 * AH + BC.
- AN = (AD - BC) / 2.
Vi ersätter numeriska värden:
- AN = (65-51) / 2 = 7.
Med hjälp av Pythagoras teorem söker vi höjden på BH:
- AV² = ВН² + АН².
- VN = √ (AV² - AN²) = √ (25² - 7 ²) = √ (625-49) = √576 = 24
Hur man hittar sinus av trapetsvinkeln
Leta nu efter sinusens akuta vinkel:
- sinBAH = BH / AB.
Vi ersätter numeriska värden:
- sinBAH = 24/25 = 0.96.
svar:
- sinBAH = 0,96.