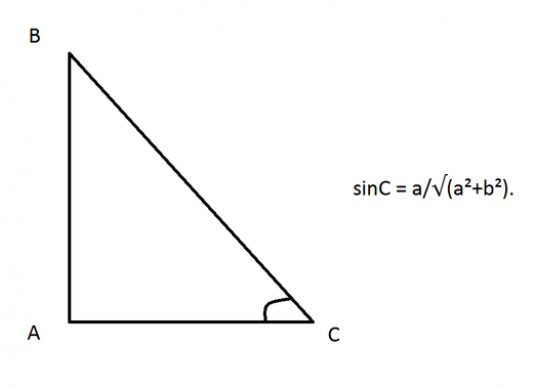Hur hittar man det yttre hörnet?

Sinvinklarna behöver inte beräknasbara i en rätt triangel, men i någon annan. För att göra detta, håll triangel höjd (vinkelrätt mot en av parterna, utelämnas från motsatt vinkel) och lösa problemet för en rätvinklig triangel, med användning som en av benen höjd.
Hur man hittar sinusen i det yttre hörnet av en triangel
Först måste du förstå vad ett yttre hörn är. Vi har en godtycklig triangel ABC. Om en av sidorna, till exempel AC, fortsätter bortom BAC-vinkeln och drar en AO-stråle, kommer den nya OAB-vinkeln att vara extern. Här kommer vi leta efter sin sinus.
För att lösa problemet måste vi släppa den vinkelräta bromsen till sidan av AU från vinkeln ABC. Detta är höjden på triangeln. Lösningen av problemet kommer att bero på vad vi vet.
Det enklaste alternativet är om du vet vinkeln på DIG. Då löses lösningen extremt enkelt. Eftersom strålen OC är en rak linje, är vinkeln OAC = 180 °. Följaktligen är vinkeln OAB och BAC intilliggande, och sinesna i angränsande vinklar är lika stora.
Låt oss överväga ett annat problem: I en godtycklig triangel ABC är sidan känd: AB = a och höjden BH = h. Det är nödvändigt att hitta sinus i OAS-vinkeln. Eftersom vi nu har en rektangulär triangel ABN, kommer vinkeln ABNs sinus att vara lika med förhållandet mellan HH-benet och hypotenuse AB:
- sinBAH = BH / AB = h / a.
Detta är också enkelt. Ett mer komplicerat problem, om höjden h är känd och sidorna AC = c, BC = b, är det nödvändigt att hitta sinus av vinkeln OAB.
Genom pythagorasatsen finner vi katetern av CH av triangeln VSN:
- BC² = BH2 + CH2 b2 = h2 + CH2,
- CH² = b ^ - H², CH = √ (b ^ - H²).
Härifrån kan du hitta ett segment av AS-sidan av växelriktaren:
- AH = AC - CH = c - √ (b² - h²).
Nu använder vi igen Pythagoras teorem för att hitta den tredje sidan av AV-triangeln ABN:
- AB² = BH2 + AH² = h2 + (c - √ (b² - h²)) ².
BAC-vinkelns sinus är lika med förhållandet mellan höjden på HV för triangeln och sidan AB:
- sinBAC = BH / AH = h / (c - √ (b2 - h2)).
Eftersom vinklarna OAB och BAC är angränsande är deras sines lika stora.
Således kombinerar den pythagoranska stolen, definitionensinus och några andra ståndpunkter (i synnerhet i angränsande vinklar), är det möjligt att lösa nästan de flesta problem på trianglar, inklusive att finna sinus av den yttre vinkeln. Ibland kan ytterligare konstruktioner vara nödvändiga: att dra en höjd från önskad vinkel, för att fortsätta sidan av hörnet bortom dess gränser och så vidare.