Hur hittar man trapezans höjd?

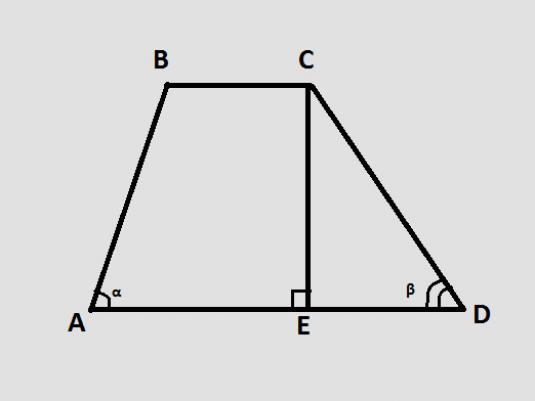
En trapezoid är en fyrkantig, tvåvars sidor är parallella (dessa är baserna för trapezoiden, som anges i figurerna a och b), och de andra två är inte (i figuren AD och CB). Trapezans höjd är segmentet h ritat vinkelrätt mot baserna.

Hur hittar man trapezens höjd för känt trapezium och baslängder?

För att beräkna området S för trapesformiga ABCD använder vi formeln:

S = ((a + b) × h) / 2.

Här är segmenten a och b grunden för trapezan, h är trapezens höjd.

Konvertera denna formel, vi kan skriva:

h = 2 × S / (a ​​+ b)

Med hjälp av denna formel erhåller vi värdet av h om området S och längderna av baserna a och b är kända.

exempel

Om det är känt att området för trapezoiden S är 50 cm² är längden på basen a 4 cm, längden på basen b är 6 cm, för att hitta höjden h, använder vi formeln:

h = 2 × S / (a ​​+ b);

Vi ersätter de kända kvantiteterna i formeln.

h = (2x50) / (4 + 6) = 100/10 = 10 cm

Svar: Trapezons höjd är 10 cm.

Hur kan jag hitta trapezans höjd om trapezoområdet och längden på mittlinjen ges?

Vi använder formeln för beräkning av trapesformen:

S = m × h,

Här är m mittlinjen, h är trapezens höjd.

Om frågan uppstår, hur man hittar trapezans höjd, formeln:

h = S / m, kommer att vara svaret.

Således kan vi hitta trapeziumhöjden h, med kända värden för området S och segmentet av mittlinjen m.

exempel

Trapeziummellens längd är känd, vilken är 20 cm och området S, som är 200 cm2. Låt oss hitta värdet på höjden på trapezidh.

h = S / m.

Genom att ersätta värdena S och m får vi:

h = 200/20 = 10 cm

Svar: Trapezons höjd är 10 cm

Hur man hittar höjden på en rektangulär trapezoid?

Om trapezoiden är en fyrkant, med tvåparallella sidor (baser) av trapezoiden. Diagonalen är ett segment som förbinder två motsatta vinklar av trapesformiga vinklar (segmentet AC i figuren). Om trapezoiden är rektangulär, använder vi diagonalen, höjden på trapezoiden h.

En rektangulär trapezoid är en trapezoid så att en av sidosidorna är vinkelrätt mot baserna. I detta fall sammanfaller dess längd (AD) med höjden h.

Således överväga den rektangulära trapetsformiga ABCD,där AD är höjden, DC är basen, AC är diagonalen. Vi använder den pythagoranska stolen. Kvadraten av hypotenus AC av den rektangulära triangeln ADC är lika med summan av kvadraterna på benen AB och BC.

Då kan vi skriva:

AC² = AD² + DC².

AD är trekantens kateter, sidan av trapezoiden och samtidigt dess höjd. När allt kommer omkring är segmentet av AD vinkelrätt mot baserna. Dess längd kommer att vara:

AD = √ (AC² - DC²)

Så, vi har en formel för beräkning av höjden av trapezium h = AD

exempel

Om längden på basen av den rektangulära trapezoiden (DC) är 14 cm och diagonalen (AC) är 15 cm, kommer vi att använda Pythagoreas teorem för att få höjden (AD-sidan).

Låt x vara ett okänt ben av en högra triangel (AD) då

AC² = AD² + DC² kan spelas in

15 ² = 14 ² + ² ²,

х = √ (15 ²-14 ²) = √ (225-196) = √29 cm

Svar: Höjden på den rektangulära trapezoiden (AB) kommer att vara √29 cm, vilket är cirka 5,385 cm

Hur man hittar höjden på en isosceles trapezoid?

En isosceles trapezoid kallas en trapezoid, yLängden på sidosidorna är lika med varandra. En rätlinje som dras genom mitten av basen av en sådan trapezform kommer att vara symmetriaxeln. Ett speciellt fall är trapezoiden, vars diagonaler är vinkelräta mot varandra, då är höjden h lika med halva summan av baserna.

Låt oss överväga fallet om diagonalerna inte ärär vinkelräta mot varandra. I den liksidiga (isosceles) trapezoiden är vinklarna vid baserna och längderna av diagonalerna lika. Det är också känt att alla hörn av en liksidig trapezoid rör vid en cirkellinje som dras runt detta trapezium.

Tänk på ritningen. ABCD är en isosceles trapezoid. Det är känt att basen av trapets parallella organet, BC = b parallell AD = a, sidan AB = CD = c, sedan, hörnen på baserna respektive, kan skrivas vinkel BAQ = CDS = α, och vinkeln ABC = BCD = β. Därför avslutar vi om jämlikhet triangeln ABQ triangel SCD, klipp

AQ = SD = (AD-BC) / 2 = (a-b) / 2.

Med villkoret för problemet och ett basvärde b, och sidolängden s, finner vi trapetsoid höjd h, som är lika med segmentet BQ.

Tänk på rätt triangel ABQ. BO är trapesens höjd, vinkelrätt mot basen AD, och därmed till segmentet AQ. Sidan AQ i triangeln ABQ finner vi, med hjälp av den formel som vi tidigare har erhållit:

AQ = (a - b) / 2.

Med värdena på de två benen i en högra triangel finner vi hypotenus BQ = h. Vi använder den pythagoranska stolen.

AB² = AQ² + BQ²

Vi ersätter uppgiftsuppgifterna:

c² = AQ² + h².

Vi får en formel för att hitta höjden av en isosceles trapezoid:

h = √ (c²-AQ²).

exempel

Givet en isosceles trapezoid ABCD, där basenAD = a = 10cm, basen BC = b = 4cm, och sidan AB = c = 12cm. Under sådana förhållanden, låt oss överväga, till exempel, hur man hittar trapesen i höjd, en jämn trapezoid av en ABCD.

Vi finner sidan AQ i triangeln ABQ, ersätter kända data:

AQ = (a-b) / 2 = (10-4) / 2 = 3 cm.

Nu ersätter värdena på sidorna av triangeln i formeln för den pythagoranska stolen.

h = √ (c²- AQ²) = √ (12² - 3 ²) = √135 = 11,6 cm.

Svar. Höjden h för isosceles trapezoid ABCD är 11,6 cm.