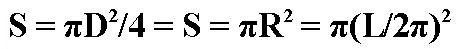Hur beräknar du en rektangelarea?

En av de viktigaste reglerna för trigonometri är beräkningen av arean av olika figurer, så många tänker på hur man beräknar rektangelområdet.

Det är värt att notera att man känner till de olika värdena: sidor, diagonaler, vinklar och omkretsar av figuren - du kan beräkna sitt område.

Område på två sidor

I uppgiften är det nödvändigt att hitta rektangelområdet om två sidor är kända: ena sidan är 3 cm och den andra sidan är 2 cm.

lösning:

Genom att komma från områdesformeln S = a * b får vi att rektangelområdet i detta fall är lika med:

• S = 3 * 2 = 6 cm ^

Svar: S = 6 cm²

Rektangelens område med känd sida och diagonal

För att lösa problem med sådana förhållanden är det nödvändigt att återkalla Pythagoras ståndpunkt.

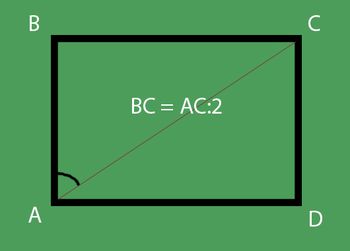
Till exempel i uppgiften är det nödvändigt att hitta rektangelns ABCD-område, när det är känt att sidan av rektangeln AB = 3 cm och den intilliggande diagonala AC = 5 cm.

lösning:

Först måste du känna till den andra sidanrektangel. För att göra detta, använd Pythagoras sats: a2 + b² = c². Med utgångspunkt från teorin får vi att sidan BC kan beräknas på följande sätt:

• solen²= AC²-av² = (25-9) = 16 cm.
• BC = 4 cm.

Således kan du definiera det önskade värdet:

• S = AB * BC = 12 cm²

Svar: S = 12 cm²

Hitta en diagonal av en rektangel finns i artikeln Hur hittar du en diagonal av en rektangel.

Område diagonalt och hörn

I uppgiften är det nödvändigt att hitta rektangelens område om diagonalen är 10 cm och vinkeln på diagonalen till rektangelns bredd är 60 grader.

lösning:

Eftersom vinkeln mellan ena sidan och diagonalen är 60 grader är rektangeln uppdelad i två trianglar. Med formeln S = 1/2 d²* sin α, vi definierar:

• S = 1/2 * 10²* sin60 ° = 50 * (√3) / 2 cm² = 25 * (√3) cm²

Svar: S = 25 * (√ 3) cm².

Området av rektangeln längs omkretsen och sidan

Det är nödvändigt att hitta rektangelområdet när det är känt att sidan är 5 cm och omkretsen är 30 cm.

lösning:

För att hitta rektangelområdet måste du bestämma längden på dess andra sida. Om vi ​​känner till omkretsen i problemet, då, baserat på formeln för att hitta

perimeter: P = 2 (a + b), vi kan beräkna att den andra sidan av rektangeln kommer att vara lika med:

• b = (P-2a) / 2 = (30-10) / 2 = 10 cm.

Således kan rektangelens area beräknas från den redan kända formeln:

• S = a * b, det vill säga
• S = 5 * 10 = 50 cm ^.

Svar: S = 50 cm².

Att känna till de grundläggande formlerna, liksom de nödvändiga mätningarna (sidor, perimeter, diagonaler och vinklar), kan du alltid bestämma och hitta rektangelområdet.

Om du behöver hitta en kvadratkvarter, läs om den i artikeln Hur hittar du en kvadrat.

Formlerna för att hitta områdena med olika figurer finns i artikeln Hur hittar du en siffra.