Vad är längden på rektangeln?

Problemet med att hitta längden på en rektangel kanformuleras på olika sätt. Låt oss räkna ut hur man finner längderna på sidorna av en rektangel för varje speciell formulering. Längden på rektangeln är dess långsida, rektangelens bredd, dess korta sida.

• En rektangel ges. Värdet av dess omkrets P är känt, rektanglets bredd B är känd. Det är nödvändigt att hitta längden på rektangeln.

  Omkretsen P är summan av längderna på alla sidor av rektangeln. Låt L vara den okända längden på rektangeln. Då P = 2B + 2L. Därmed: 2L = P-2B. L = (P-2B) / 2.

• En rektangel ges. Värdet av dess område S är känt. Bredden på rektangeln B är känd. Det är nödvändigt att hitta längden på en rektangel.

  Området av rektangeln är produkten av dess längd efter bredd. Låt L vara den okända längden på rektangeln. Sedan S = L * B. Därför vet vi hur rektanglängden är lika med: L = S / B.

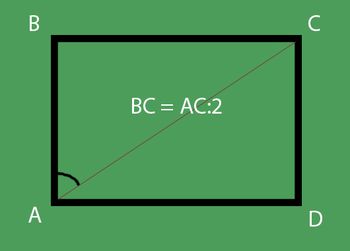
• En rektangel ges. Vi känner till värdet av rektangulans B bredd och längden på diagonal A. Det är nödvändigt att veta hur länge rektangeln är lika med.

  När en rektangel är uppdelad av en diagonal, detbestår av två rektangulära trianglar. För en rätvinklig triangel är den pythagoranska ståndpunkten giltig: "Hypotenusens kvadrat är lika med summan av benens kvadrater". I detta speciella fall är benen rektangelens bredd och längden på rektangeln L. Hypotenusen är rektangelens diagonal. Analysera alla ovanstående får vi: A²= B²+ L². Därmed L²= A²- B². L = v (A²-B²).

• En rektangel ges. Längden på rektangelens diagonala är känd. Är det känt vilken vinkel? bildar en diagonal med en rektangel bredd. Hitta längden på rektangeln.

  Diagonalen delar rektangeln i tvårätt triangel. Därför ger förhållandet mellan rektanglängden och dess diagonala en sinus med känd vinkel. Följaktligen: synd a = L / A, här är L rektanglängden. L = sin a / A

• En rektangel ges. Längden på rektangelens diagonala är känd. Är det känt vilken vinkel? bildar en diagonal med längden på en rektangel. Hitta längden på rektangeln.

Eftersom diagonalen, bredden och längden av rektangelnbildar en rektangulär triangel, så innehåller följande uttryck: cos a = L / A, d.v.s. Förhållandet mellan längden av rektangeln och dess diagonala ger cosinusen med den kända vinkeln. L = cos a / A.

Vi lärde oss hur man hitta längden på en rektangel förav alla möjliga formuleringar av problem (om kanten och bredden är kända, om området och bredden är kända, om diagonalen och vinkeln är kända, om diagonalen och bredden är kända). Ersätt kända värden och få ett tillförlitligt svar.