Hur kan jag hitta en rektangels bredd?

Att lösa problem med quadrangles är en avDe mest omfattande sektionerna av geometri, vilket ger skolbarn många svårigheter. Vi föreslår att du hanterar typiska uppgifter där du vill hitta bredden på en rektangel.

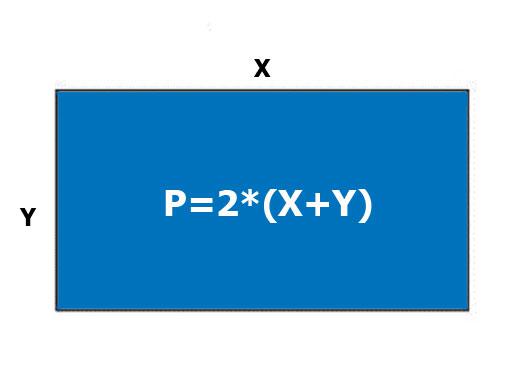
Först och främst är det nödvändigt att komma ihåg vilken typ avfigur och vilka är dess huvudegenskaper. En rektangel är en fyrkantig med alla sina vinklar raka, och motsatta sidor är lika. Den horisontella sidan kallas rektangelens bredd, och den vertikala sidan kallas längden.

Problem 1. Beräkna bredden, känner till omkretsen

Låt oss analysera denna typ av uppgift med exemplet på följande uppgift. Rektangel, omkrets

som är 36 cm och längden är 16 cm. Det är nödvändigt att hitta bredden. Omkretsen är summan av sidorna av figuren. Eftersom de motsatta sidorna av rektangeln är lika har formeln av dess omkrets följande form: P = 2 (a + b), där a och b är rektangelens sidor.

Vi får:

b = P: 2 - a = 36: 2-16 = 2 (cm)

Svar: Rektangelens bredd är 2 cm.

Problem 2. Hitta bredden, känna längden och omkretsen

Låt oss lätt komplicera uppgiften. Nu befinner bredden av rektangeln, om det är känt att det är 5 gånger mindre än dess längd och omkrets av triangeln är lika med 120 cm.

Från problemet med problemet:

a = 5b

Vi vet redan att b = P: 2 - a. Vi ersätter värdena för P och a. Vi får:

b = 120: 2-5b;
6b = 60;
b = 60: 6
b = 10 (cm).

Svar: Rektangelens bredd är 10 cm.

Problem 3. Bestäm bredden om området är känt

Uppgiftstillstånd: Trädgården har en rektangulär form. Området är 400 000 m2 och längden är 400 m. Vad är trädens bredd?

En grönsaks trädgård är en rektangel. Området av en rektangel är lika med produkten av dess sidor. Om vi känner till längden och arean är bredden lika med:

b = P: a = 400 000: 400 = 1000 (m)

Svar: Bredden på trädgården är 1000 m.

Problem 4. Hur man hittar bredden, känner till diagonalen

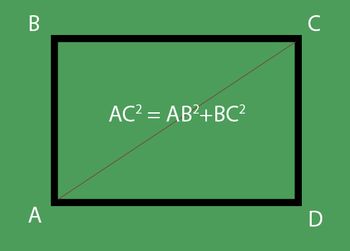
Denna uppgift är redan lite mer komplicerad än de tidigare. I den, förutom egenskaperna hos en rektangel, är det nödvändigt att erinra om de formeln rektangulära trianglar. Antag att AC diagonalen av rektangeln AVSD lika med 54,6 cm, och längden bredd-förhållande - 16: 9. Det är nödvändigt att hitta bredden på figuren.

Triangeln ABC har en rätt vinkel, vilket betyder att den är rektangulär. Diagonalen är dess hypotenus och sidorna är benen.

Från villkoret:

16AB = 9BC, följaktligen AB = 9BC: 16

Genom den pythagoranska stolen:

AS² = AB²+ Sön²

Vi ersätter numren:

54,62 = (9BC: 16)²+ Sön²
2981,16 = 81BC²: 256 + sön²
2981,16 = 337BC²: 256
337VS² = 763176,96
solen² = 2264,62
VS = 47,59 (cm)

Svar: Triangeln är 47,59 cm bred.

Problem 5. Diagonal och vinkel

Rektangel för ABCD visas, vars diagonala är 8 cm och vinkeln är 30 grader. Det är nödvändigt att hitta rektanglets bredd.

Lösning: eftersom vinkeln ABC är rak, är triangeln ABC rektangulär,

hypotenus och AB och BC är benen. Det är känt att katetan, som ligger mot 30 graders vinkel, är lika med hälften av hypotenusen. Det visar sig

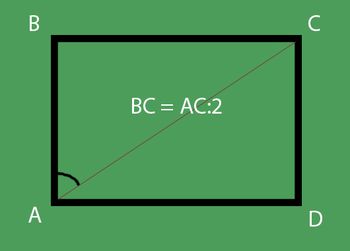
BC = AC: 2 = 8: 2 = 4 (cm)

Svar: Rektangelens bredd är 4 cm.

Som du kan se är typiska uppgifter för att hitta en rektangels bredd ganska enkla. Det viktigaste är att känna formlerna och egenskaperna hos en rektangel och rektangulära trianglar.

Om du vill hitta längden på en rektangel, läs artikeln - Vad är längden på rektangeln.

Läs mer: