Hur hittar man omkretsen och området?

Intressant, många år sedan en sådan sektionmatematik, som "geometri" kallades "landmätning". Och hur man hittar omkretsen och området, det är känt under lång tid. Till exempel säger de att de allra första räknarna av dessa två kvantiteter är folket i Egypten. Tack vare sådan kunskap kunde de bygga de kända byggnaderna idag.
Möjligheten att hitta området och omkretsen kananvändbart i vardagen. I vardagen används dessa värden när det är nödvändigt att måla, plantera eller bearbeta trädgården, tapeter i rummet etc.
omkrets
Oftast är det nödvändigt att ta reda på omkretsenpolygoner eller trianglar. För att bestämma detta värde är det bara nödvändigt att känna längden på alla sidor, och omkretsen är deras summa. Hitta omkretsen, om området är känt, är det också möjligt.
triangel
Om du behöver veta omkretsen av en triangel, fördess beräkning är det nödvändigt att tillämpa en sådan formel P = a + b + c, där a, b, c är sidorna av triangeln. I detta fall summeras alla sidor av en vanlig triangel i planet.
runda
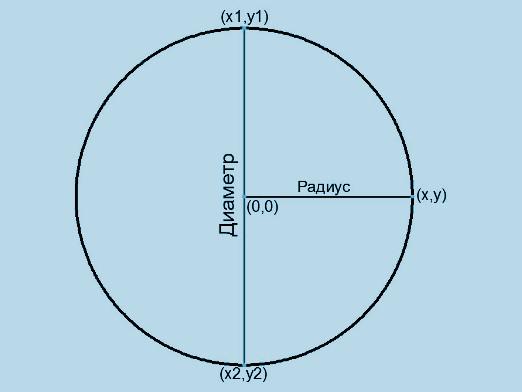
Omkretsen av en cirkel kallas vanligtvis längdencirkel. Att hitta detta värde, är det nödvändigt att använda formeln: L = π * D = 2 * π * r, där L- omkrets, r - radien, D - diameter och antalet π, såsom är känt, är ungefär lika med 3,14.
Kvadratisk, diamant
Formler för omkretsen av en kvadrat och en diamantär desamma, eftersom både en figur och den andra alla sidor är lika. Eftersom torget och rhombuset har lika sidor kan deras (sidor) betecknas med ett bokstav "a". Det visar sig att omkretsen av en kvadrat och en diamant är lika med:
- P = a + a + a + a eller P = 4a
Rektangel, parallellogram
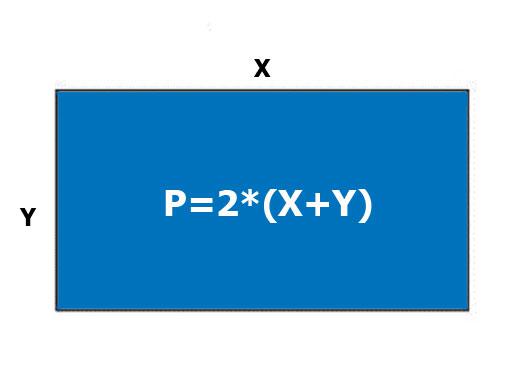
När det gäller en rektangel och parallellogram är de motsatta sidorna desamma, så de kan betecknas med två olika bokstäver "a" och "b". Formeln ser så här ut:
- P = a + b + a + b = 2a + 2b. Två kan härledas från parentes, och följande formel erhålls: P = 2 (a + b)
trapets
Vid trapesen är alla sidor olika, därför betecknas de av olika bokstäver i det latinska alfabetet. I detta avseende ser formeln för trapezets omkrets ut så här:
- P = a + b + c + d Här sammanfattas alla sidor ihop.
För mer information om beräkning av omkretsen, se Hur hittar du omkretsen.
område
Område - den delen av figuren som är innesluten i sin kontur.
rektangel
För att beräkna området av en rektangel,det är nödvändigt att multiplicera värdet på en sida (längd) med värdet av det andra (bredd). Om längden och breddvärdena betecknas med bokstäverna "a" och "b", beräknas området med formeln:
- S = a * b
kvadrat
Som redan känt är sidorna på torget lika, så att beräkna området kan du helt enkelt ta en sida i en kvadrat:
- S = a * a = a2
romb
Formeln för att hitta rhombusområdet har en något annorlunda form: S = a * hen, där hen Är längden på diamantens höjd, vilken dras mot sidan.
Dessutom kan diamantens område hittas med formlerna:
- S = a2* sin α, medan a är sidan av figuren, och vinkeln a är vinkeln mellan sidorna;
- S = 4r2/ sin a, där r är cirkelns radie inskriven i diamanten och vinkeln a är vinkeln mellan sidorna.
runda
Området i cirkeln är också lätt igenkänt. För att göra detta kan du använda formeln:
- S = πR2, där R är radie.
trapets
För att beräkna området för trapezoiden kan du använda följande formel:
- S = 1/2 * a * b * h, där a, b är basen av trapezoiden och h är höjden.
triangel
För att hitta området i en triangel, använd en av flera formler:
- S = 1/2 * a * b sin α (där a, b är sidorna av triangeln och α är vinkeln mellan dem);
- S = 1/2 a * h (där a är basen av triangeln, h är höjden sänkt till den);
- S = abc / 4R (där a, b, c är sidorna av triangeln, och R är radien för den omkretsade cirkeln);
- S = p * r (där p är halvperimetern, r är den inskrivna cirkelns radie);
- S = √ (p * (p-a) * (p-b) * (p-c)) (där p är semiperimetern, a, b, c är sidorna av triangeln).
parallellogram
För att beräkna området för en given figur måste du ersätta värden i en av formlerna:
- S = a * b * sin α (där a, b är basen av parallellogrammet, α är vinkeln mellan sidorna);
- S = a * ha (där a är parallellogrammets sida, hen Är parallellogrammets höjd, vilken sänks till sidan a);
- S = 1/2 * d * D * sin α (där d och D är parallellogrammets diagonaler och α är vinkeln mellan dem).