Hur hittar man en diamanthöjd?

En rhombus är en fyrkantig, där alltingSidorna är lika och motsatta sidor är parallella. Detta villkor förenklar formlerna för bestämning av höjden - vinkelrätten sjönk från hörnet till ena sidan. I en fyrkant från varje hörn kan du sänka höjden på två sidor. Tänk på hur man hittar rhombusens höjd, hur de relaterar till varandra.

Hur man hittar höjden på en diamant

Fyrhjulingar är sådana siffror, för vilkaVinklarna kan variera med konstanta längder på sidorna. Därför är det, i motsats till en triangel, inte tillräckligt att veta längderna på sidorna av en fyrkant, är det nödvändigt att ange dimensionerna för vinklarna eller höjden. Till exempel, om diamanterna är 90 °, erhålls en kvadrat. I detta fall sammanfaller höjden med sidan. Tänk på hur man hittar diamantens höjd i andra vinklar än raka linjer.

Vi bestämmer värdet av diamantens två höjder tappade från ett hörn

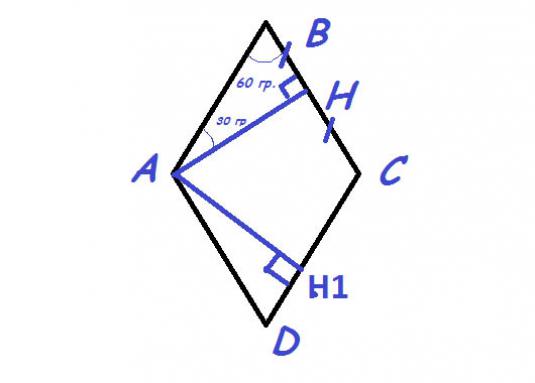
Vi har en rhombus ABCD, för vilken AB // CD, BC // AD, AB =BC = CD = DA = a. Höjden h är den vinkelräta föll från hörnet till motsatt sida. Vi sänker höjden AH till sidan BC, och den andra höjden AN1 tappas från samma vinkel till sido-DC.

• Då höjden AN = AB × sin∟B;
• Höjd AH1 = AD × sin∟D.

En av egenskaperna hos rhombus är motsatsens jämlikhetvinklar, jag. ∟ B = ∟D. Eftersom AB = AD (alla sidor av rhombus är alla lika med varandra), då höjden AH = AH1. På samma sätt kan det visas att två höjder utelämnas från vilken vinkel som helst, är lika med varandra.

Hur korrelerar de andra diametrarna i rhombus med varandra?

Eftersom motsatta sidor är parallella är summan av vinklarna intill ena sidan 180 °. Följaktligen är sinesna i alla fyra vinklarna lika varandra:

• sin∟D = sin (180 ° - ∟D) = sin∟C = sin∟A = sin∟B.

Följaktligen utesluter alla höjder från någonav rhombusen är lika med varandra, och sidan, vinkeln och höjden är sammankopplade med ett styvt förhållande: h = a × sin∟A, där a är längden på någon sida och ∟A är någon rhombusvinkel.