Hur hittar man en vinkel av en likvärdig triangel?

En likvärdig triangel är aDen enklaste polygonen har tre vinklar och tre sidor. Innan du räknar ut hur du hittar vinklarna i en likriktad triangel måste du veta egenskaperna för denna geometriska figur.

Egenskaper av en isosceles triangel

Låt oss överväga egenskaperna hos en likvärdig triangel.

• I en likriktad triangel är de båda sidorna lika. Den tredje parten är grunden.
• Vinklar vid basen av en sådan triangel är lika.
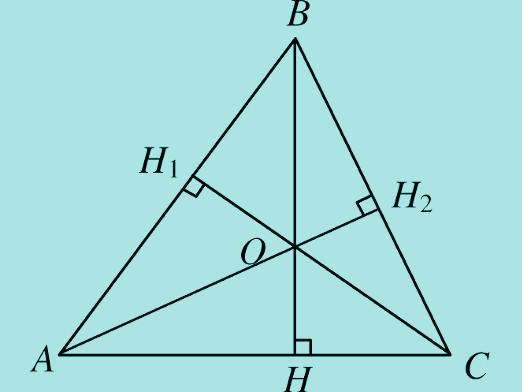
• Bisektris, median och höjden dras från hörnen till den motsatta sidan av de geometriska formerna och är alltid lika.
• Bisektorn, medianen och höjden från det övre hörnet till basen av isosceles triangeln sammanfaller.
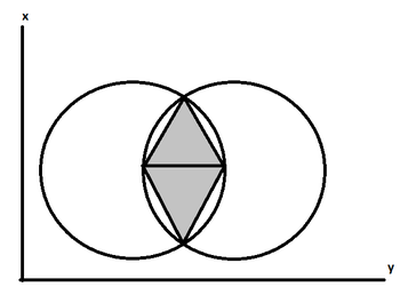
• Om inom en liksidig triangel inskriven cirkel, samt beskriva det runt denna siffra, deras centra ligger på samma linje.
• Hjulen vid basen kan bara vara skarpa.

Således, om de två hörnen av triangeln är lika, och dess höjd sammanfaller med median bisektrisen och det är likbent. Detta är huvudskylten på en likriktad triangel.

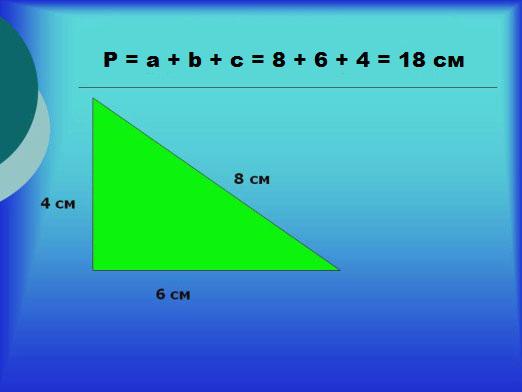
Nu överväga hur man hittar vinklarnaen likriktad triangel. Om en sådan triangel också är rektangulär är det inte svårt att hitta två av sina vinklar, så de kommer alltid att vara lika med 45 grader, vilket följer av egenskaperna och tecknen på en likriktad triangel.

• Att veta en av vinklarna, kan du alltid beräknabehövs. Till exempel kommer vinkeln vid basen att betecknas med bokstaven a, vinkeln på vertexen av figuren kommer att betecknas med bokstaven P. Följaktligen är vinkeln a lika med: (π - β) / 2, där π är en konstant.
• Vinklar kan också beräknas från arcsiner. För detta ändamål är det nödvändigt att beskriva en sådan triangel runt cirkeln med en radie som är betecknad med en stor bokstav R. Därefter vinkeln α = arcsin (a / 2R), och vinkeln β = arcsin (b / 2R), där a och b är de sidor av en triangel.

Exempel på lösning av problemet

Behöver hitta vinklar likbent triangel, om det är känt att vinkeln vid sin bas genom 15 grader större än den vinkel som är motsatt basen.

Lösning: Beteckna motsatt vinkel β, då vinkeln i botten blir: β + 15. Eftersom summan i triangeln alltid är 180 grader finner vi:

p + 2x (p + 15) = 180;

p + 2p + 30 = 180;

3 p = 180-30;

3 p = 150;

p = 50

Så vinkeln på botten är 50 grader, ochdå är de andra två vinklarna lika med 65 grader vardera. Nu vet du reglerna för hur man hittar vinklarna av en likvärdig triangel. Vi önskar er lycka till i alla beräkningar!