Hur hittar man en parabola?

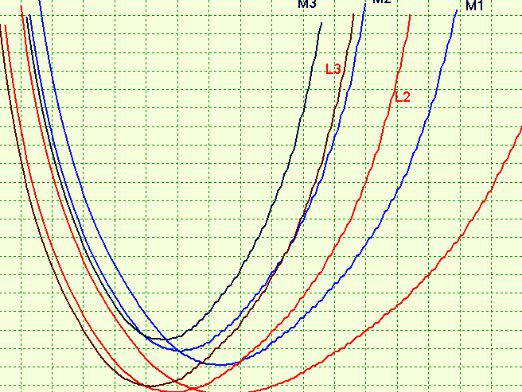
En parabol är en graf för en kvadratisk funktion. Denna rad har en betydande fysisk betydelse. För att göra det lättare att hitta en parabolas toppunkt måste du rita den. Sedan på diagrammet kan du lätt se toppen. Men för att bygga en parabola är det nödvändigt att veta hur man hittar punkterna i en parabola och hur man hittar koordinaterna för en parabola.

Vi hittar punkterna och toppunktet hos parabolen

I den allmänna representationen har den kvadratiska funktionen följande form: y = ax²+ bx + c. Diagrammet för denna ekvation är en parabola. Om a> 0, är ​​dess grenar riktad uppåt och för en <0 - ner. För att konstruera en parabola på ett diagram är det nödvändigt att känna till tre punkter om det passerar längs ordinataxeln. Annars bör fyra byggnadspunkter vara kända.

När hitta abskissan (x) är nödvändigt för att ta koefficienten för den (x) polynom med en given formel, sedan dividera med den dubble koefficient (x²), multiplicera sedan med ett tal - 1.

För att hitta ordinaten är det nödvändigt att hitta diskriminanten, multiplicera den med - 1, dividerar sedan med koefficienten vid (x²) först multiplicera den med 4.

Vidare, utbyte av numeriska värden beräknas detvertex av en parabola. För alla beräkningar är det önskvärt att använda en ingenjörsberäknare, och när man ritar diagram och paraboler för att använda en linjal och ett diagram, kommer detta avsevärt att förbättra noggrannheten i dina beräkningar.

Tänk på följande exempel, vilket hjälper oss att förstå hur man hittar en parabolas toppunkt.

x²-9 = 0. I detta fall är de vertex koordinater beräknas på följande sätt: Punkt 1 (-0 / (2 * 1) och punkt 2 - (0 ^ 2-4 * 1 * (- 9)) / (4 * 1)). Sålunda är koordinaterna för vertexet värdena (0; 9).

Hitta abtexen av vertexen

När du har lärt dig hur man hittar en parabola, och du kan beräkna punkterna i korsningen med koordinataxeln (x), kan du enkelt beräkna toppunktets abscissa.

Antag att (x₁) och (x₂) är rötterna till en parabola. Parabolens rötter är punkterna i dess korsning med abscissaaxeln. Dessa värden blir till noll en kvadratisk ekvation av följande formulär: ax² + bx + c.

I detta fall | x₂| | > | x₁|, sedan är parabolens toppunkt beläget i mitten mellan dem. Således kan den hittas med följande uttryck: x₀ = ½ (| x₂| | - | x₁|).

Hitta området i figuren

Att hitta ytan av en siffra på en koordinatdu behöver veta integralet. Och för att tillämpa det är det tillräckligt att känna till vissa algoritmer. För att hitta det område som avgränsas av paraboler, är det nödvändigt att producera sin bild i ett kartesiskt koordinatsystem.

Först, enligt den ovan beskrivna metoden,koordinat av axelns (x) vertex, sedan axeln (y), varefter parabolens toppunkt ligger. Nu måste vi bestämma gränserna för integrationen. Som regel anges de i problemets tillstånd med hjälp av variablerna (a) och (b). Dessa värden bör placeras i de övre och nedre delarna av integralet. Ange sedan värdet på funktionen i en allmän form och multiplicera den med (dx). I fallet med en parabola: (x²) dx.

Då måste vi beräkna den antiderivativa generelltvärdet av funktionen. För att göra detta, använd ett speciellt värdebord. Att ersätta gränserna för integration är skillnad. Denna skillnad blir området.

Tänk exempel på systemet med ekvationer: y = x₂+1 och x + y = 3.

Det finns abscissor av skärningspunkten: x₁= -2 och x₂= 1

Vi antar att y₂= 3, medan y₁= x² + 1, ersätt värdena i ovanstående formel och få ett värde av 4,5.

Nu har vi lärt oss hur man hittar en parabola, och utifrån dessa data beräknar man också området i figuren som det begränsar.