Hur hittar man en cosinus av en triangel?

Cosine är en välkänd trigonometriskfunktion, vilket också är en av de grundläggande funktionerna för trigonometri. Cosinus av en vinkel i en trekant av rektangulär typ är förhållandet mellan den intilliggande triangeln och triangelns hypotenus. Oftast är definitionen av cosinus associerad med en trekant av rektangulär typ. Men det händer också att vinkeln som du vill beräkna kvadraten på triangeln typ cosinus i denna triangel av den rektangulära typen inte är inställd. Vad ska då göras? Hur hittar du cosinus av vinkeln på en triangel?

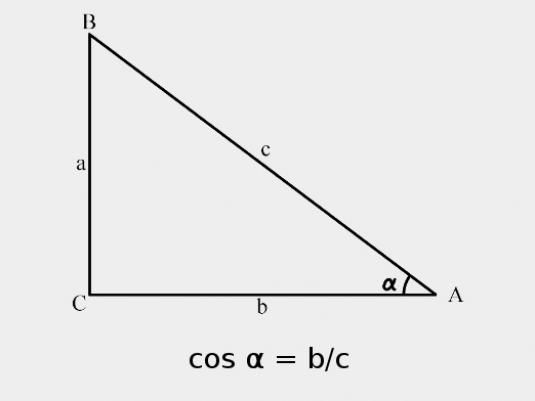
Om du vill beräkna vinkelns cosinus i exakttriangel av en rektangulär typ, då är allt väldigt enkelt. Det är bara nödvändigt att komma ihåg definitionen av kosinin, där lösningen av detta problem ligger. Det är helt enkelt nödvändigt att hitta den mycket relationen mellan det intilliggande benet och triangeln. I själva verket är det här inte svårt att uttrycka vinkelns cosinus. Formeln är följande: - cosα = a / c, här är "a" längden på benet, respektive sidan "c", längden på hypotenusen. Till exempel kan cosinus av den akuta vinkeln av en högra triangel hittas från denna formel.

Om du är intresserad av vad cosinus av vinkeln ien godtycklig triangel, då kommer cosinus teorem till hjälp, som bör användas i sådana fall. Cosinus teorem anger att kvadraten av sidan av triangeln är föregående lika med summan av kvadraterna på de återstående sidorna av samma triangel men utan den dubbla produkten av dessa sidor av cosinus av vinkeln som ligger mellan dem.

1. Om du behöver hitta cosinusen av en spetsig vinkel i en triangel, måste du använda följande formel: cosα = (a² + b² - c²) / (2ab).
2. Om i triangeln är det nödvändigt att hitta cosinus i den stumpa vinkeln, måste vi använda följande formel: cosα = (med² - a² - b²) / (2ab). Notationen i formeln - a och b - är längden på sidorna som ligger intill önskad vinkel, c är längden på sidan som ligger mitt emot önskad vinkel.

Vinkeln kan också beräknas med hjälp avsinus teorem. Hon säger att alla sidor av triangeln är proportionella mot sinus för vinklar som är motsatsen. Med användning av sinus teorem kan vi beräkna de återstående delarna av triangeln, som har endast information om de två sidorna och den vinkel som är motstående den ena sidan eller på två hörn och en sida. Tänk på exemplet. Villkor för problemet: a = 1; b = 2; c = 3. Den vinkel som är motsatt den sida av "A" betecknar - α, då, enligt formlerna har: sosα = (b ^ + C²-a ^) / (2 * b * c) = (2 ^ + 3²-1²) / (2 * 2 * 3) = (4 + 9-1) / 12 = 12/12 = 1. Svar: 1.

Om vinkelns cosinus ska beräknas inte itriangel och i någon annan godtycklig geometrisk figur blir allting lite mer komplicerat. Värdet av vinkeln måste först bestämmas i radianer eller grader, och beräkna sedan cosinus med detta värde. Cosinus av ett numeriskt värde bestäms med hjälp av Bradys tabeller, ingenjörsräknare eller speciella matematiska tillämpningar.

Särskilda matematiska tillämpningar kan haSådana funktioner som automatisk beräkning av cosines av hörn i denna eller den här siffran. Det fina med dessa program är att de ger det rätta svaret och användaren inte spendera sin tid på beslut ibland ganska komplexa uppgifter. Å andra sidan, vid konstant användas uteslutande applikationer för att lösa problem, förlorade alla färdigheter för att arbeta med att lösa matematiska problem på att hitta cosinus av vinklar i trianglar och andra godtyckliga former.